CNN
1. 합성곱 신경망(Convolutional neural network, CNN)은 시각적 영상을 분석하는 데 사용
2. 딥러닝에서 심층 신경망으로 분류
3. 시각적 영상 분석에 주로 적용
4. 상 및 동영상 인식, 추천 시스템, 영상 분류, 의료 영상 분석 및 자연어 처리 등에 응용
왜 CNN인가?
일반 DNN(Deep Neural Network)의 문제점
- 기본적으로 1차원 형태의 데이터를 사용
- 이미지가 입력값이 되는 경우, 이것을 flatten시켜서 한줄 데이터로 만들어야 함
- 이 과정에서 이미지의 공간적/지역적 정보(spatial/topological information)가 손실
- 한줄로 된 row데이터에서는 연산관계(픽셀들이 모여 객체를 만듦, 픽셀 간의 상관관계)가 제거 됨.
해결책 - CNN
- 이미지를 날것 그대로 받음(raw input)
- 공간적/지역적 정보를 유지한 채 feature들의 계층을 빌드업
- 이미지 전체보다는 부분을 보는 것, 그리고 이미지의 한 픽셀과 주변 픽셀들의 연관성을 살리는 것
- CNN은 이미지의 공간 정보를 유지하며 학습을 함
Q) 그럼 어떤 과정을 거치기에 CNN을 사용한다면 데이터 손실을 방지한 채 NN 을 구성할 수 있을까?
CNN은 featrue를 추출하는 convolution layer와 추출된 feature를 sub-sampling 하는 pooling layer로 구성
개념 정리
- feature map
- 합성곱 연산이 적용되는 객체
- 3d tensor
- 구성 : 높이, 너비, 깊이(채널)
- input feature map -> 작은 patch들 추출 -> 모든 패치에 같은 변환 적용 -> output feature map
- output feature map의 깊이(채널)는 RGB 입력처럼 특정 컬러를 의미하지 않음. filter를 의미
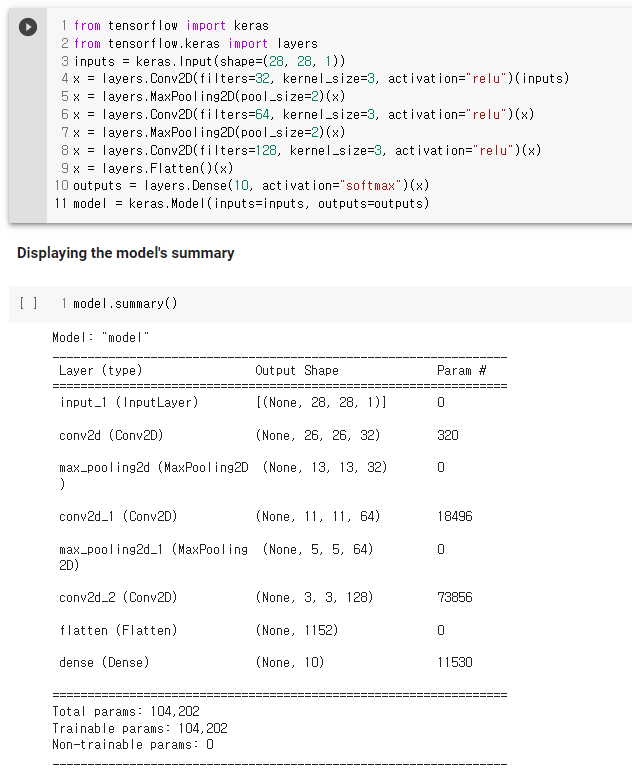
Ex)
- input feature map : (28, 28, 1), kernel size = 3
- output feature map : (26, 26, 32)
-> 입력에 대해 32개의 filter를 적용했다는 의미
-> Convolution Layer에 유입되는 입력 데이터에는 한 개 이상의 필터가 적용
-> 1개 필터는 Feature Map의 채널
-> Convolution Layer에 n개의 필터가 적용된다면 출력 데이터는 n개의 채널을 갖게 됨
-> 32개의 출력 채널은 각각 26 x 26 크기의 배열 값을 가짐(reponse map)
-> 깊이 축에 있는 각 차원은 하나의 특성(혹은 필터), 2d tensor(필터 응답을 나타냄)
- Convolution
- 요소별 연산 by filter(kernel)
Ex) 예시1
- 입력으로부터 패치를 뽑아낸다, 아래 예시1 에서 빨간색부분
- 3x3 크기의 윈도우가 슬라이딩하면서 모든 위치에서 특성 패치를 추출한다
- 3x3 필터(합성곱 커널)로 12x12 이미지에서 10x10 이미지를 생성한다
- 아래 예시에서는 필터가 3개 있음. -> 10x10 이미지 3개 생성. (10, 10, 3)
Ex) 예시 2
- input feature map에서 channel이 3인 경우
- 3차원 합성곱 연산
- 입력 데이터의 채널 수와 필터의 채널 수가 같아야 함
- 채널 수가 3인 필터
- Filter 이해
- 필터는 추출하려는 이미지의 특징이 대상 데이터에 있는지 없는지 검출해주는 함수라고 이해하면 됨
- 아래는 곡선을 검출하는 필터 -> 저 필터를 적용해서 높은 값이 나온다면? 곡선이 있다는 것!(특징 검출)
- CNN은 filter의 값을 훈련을 통해 학습한다!
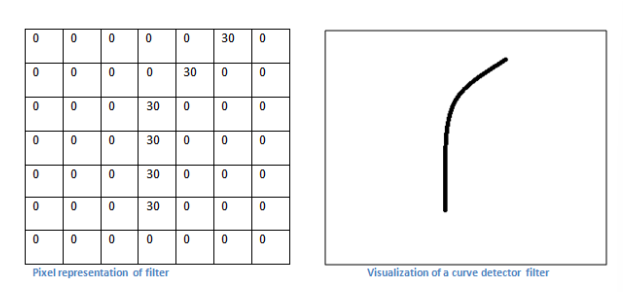
- 이미지의 곡선 부분에 필터를 적용하면 매우 높은 값이 나옴 -> 이미지에 곡선이 있다는 의미
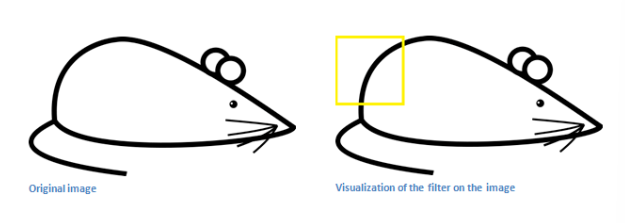

- 하지만 곡선이 없는 부분에 필터 적용하면 0에 수렴하는 값 나옴
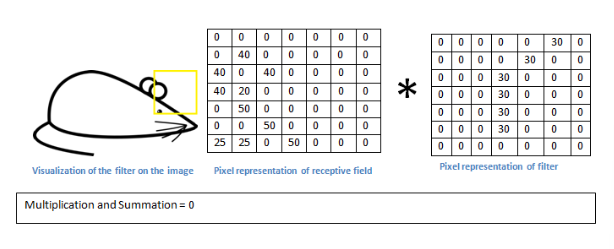
- 요약 : 필터를 통해 입력 받은 이미지에서 해당 특성을 가지고 있는지 판단할 수 있다.
- 필터를 통해 얻은 feature map의 값을 통해 대략적으로 이미지의 어느 부분에 그 특징이 있는지 판단을 할 수 있다.
- Stride
- 합성곱의 parameter
- 윈도우를 몇 칸씩 움직일 것인가.
- 두번의 연속적인 윈도우 사이의 거리
- 스트라이드 합성곱
- 다운샘플링
- 분류 모델에서는 드물게 사용(분류모델에선 스트라이드 대신 풀링을 통해 다운샘플링). 일부 유형의 모델에서는 유용.


- activation function은 언제?
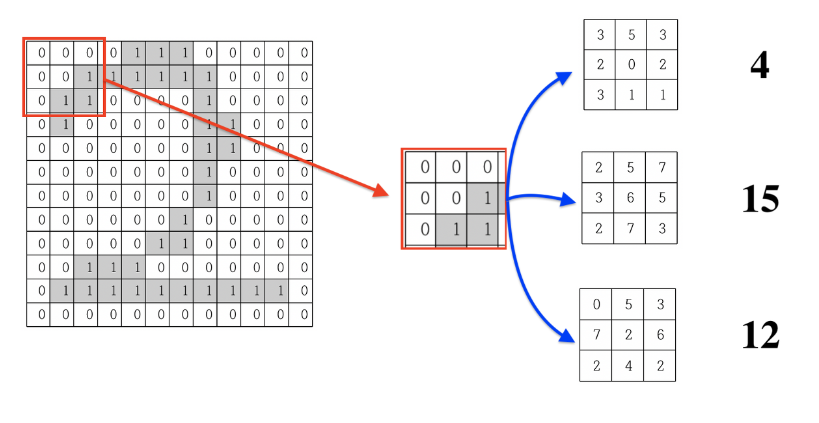
- 아래 그림은 M x N x 3인 input image에 3 x 3 x 3 filter(채널이 3인 필터)를 적용한 예시
- 합성곱 연산(convolution)을 통해 나온 값에 bias이 더해지고 그 값에 활성화 함수를 적용
- output feature map의 각 한 칸 한 칸에 활성화함수 적용
- feature map에 특징이 있으면 픽셀은 큰 값, 특징이 없으면 픽셀은 0에 가까운 값이 담겨있음
이런 정량적인 값을 비선형의 값으로 바꿔주는 과정 -> 활성화 함수
ex) 위의 쥐 예시에서 곡선필터를 적용한 결과 6600과 0의 값을 얻었다면 이러한 값들을
곡선 특징을 갖고 있다와 없다(비선형)으로 바꿔주는 과정이 활성화 함수


- relu : 모든 음수 pixel values를 0으로 대체함
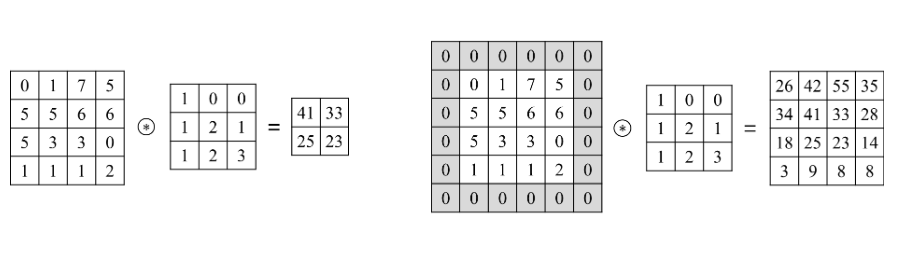
- 12x12 가 10x10으로 줄어들었는데 입력과 동일한 크기의 특성맵(feature map)을 얻고싶다면?
- padding
- 입력 특성 맵의 가장자리에 적절한 개수의 행과 열 추가
- 합성곱 이후에도 원래 크기와 동일한 이미지 유지.
- 주로 zero - padding : 0 값을 갖는 데이터 추가
- pooling
- convolution layer의 출력을 입력으로 받아서 출력 데이터의 크기를 줄이거나, 특정 데이터를 강조하는 용도
- max pooling : 입력 특성 맵에서 윈도우에 맞는 패치를 추출. 각 채널 별로 최댓값을 출력
- max외에 average pooling, min pooling도 있음

- pooling vs convolution
유사점
- 강제적으로 특성 맵을 다운샘플링한다는 점에서 유사함
차이점
- pooling은 추출한 패치에 선형 변환(합성곱 커널)을 적용하는 대신 하드코딩된 연산을 사용(ex 최댓값 추출)
- pooling은 보통 2x2 윈도우와 stride 2를 사용하여 feature map을 절반 크기로 다운샘플링 함
- 반면에 합성곱은 전형적으로 3x3윈도우와 stride 1을 사용
Flatten
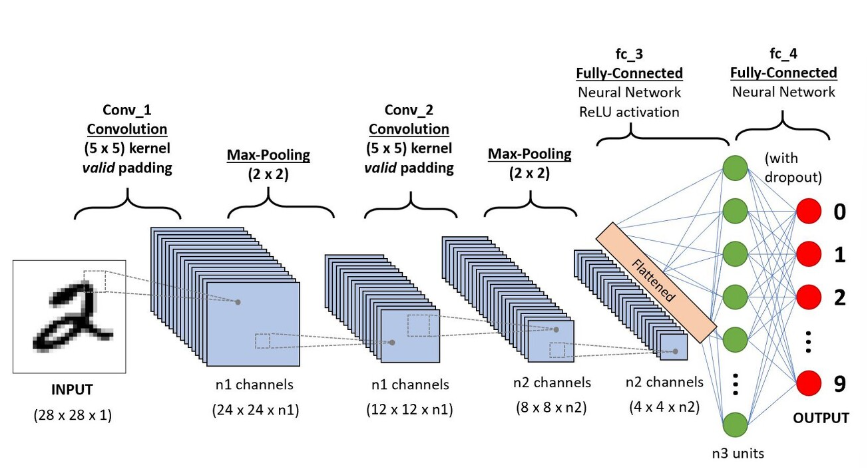
- 아래 그림은 전체 CNN의 과정
- convolution과 pooling을 반복하면서 이미지의 수는 점점 많아지고 크기는 점점 줄어들게 됨
- 최종적으로 도출된 n x n 이미지는 이미지라는 의미보단 특정 이미지에서 얻어온 하나의 특이점 데이터가 됨
- 2차원이 아니라 1차원의 row data로 취급해도 무관한 상태가 된다는 의미(Flatten)
- (None, 3, 3, 128) -> (None, 1152), 1152 = 3 x 3 x 128
- Flatten : 하나의 이미지로부터 다양한 특이점들을 뽑아내고 이것을 1차원의 데이터로 변형하는 것
- 크기는 점점 작아지고, 깊이는 깊어짐
정리
Q) 그럼 어떤 과정을 거치기에 CNN을 사용한다면 데이터 손실을 방지한 채 NN을 구성할 수 있을까?
다시 처음으로 돌아와 이 질문에 대답을 해보면서 이해한 걸 요약하자면..
CNN은
입력 데이터에 대해서 필터를 통해 이미지의 특징을 추출하고(Convoluiton layer)
특징을 강화하고 이미지의 크기를 축소한다(Pooling layer)
그리고 이 과정이 반복되다보면 row data로 취급할 수 있게 된다.
여기서 row data란 초반에 언급했던 단순히 이미지를 길게 늘려놓은 row data가 아닌,
CNN과정을 거치며 이미지의 특징 정보를 담고 있는 row data이다.
따라서 CNN을 사용한다면 이미지의 정보 손실을 방지한 채 NN을 구성할 수 있게 되는 것이다!
(혹시 내가 잘못이해한 게 있다면 지적 환영)
'Python > DL' 카테고리의 다른 글
| 신경망, 오차역전파법 (0) | 2023.07.14 |
|---|---|
| CNN 이해하기 (2) (0) | 2023.05.08 |
| 딥러닝의 학습 방법 (0) | 2023.03.19 |
| 활성화 함수, 과적합, 기울기 소실 (0) | 2023.03.19 |
| 퍼셉트론 , ANN vs DNN (0) | 2023.03.19 |



