서포트 벡터 머신 회귀(support vector machine regression)
- 비모수적 방법 - 커널 함수를 기반으로 함
- 제한된 마진 오류 안에서 가능한 한 많은 관측치가 마진에 포함되도록 학습하는 방법
- 마진 안에 관측치가 많은 초평면이 좋은 초평면이다
- svm과 마진을 고려하는 건 똑같지만, svr은 마진 밖에 있는 error가 최소가 되도록 동작함
- 마진의 폭은 하이퍼파라미터 ε(입실론)으로 조절(slack variable 과 혼동 x)

- 마진을 통해 오차에 반응하지 않는 영역 마련 -> 노이즈에 영향을 받지 않도록
- 마진에 들어가는 학습데이터를 추가 -> 예측 능력에 영향 X
- 모델은 입실론에 민감하지 않다
- 입실론이 아니라 규제 C에 민감하다
- SVR의 규제 C
- SVM의 슬랙의 합을 한정하는 규제 C와는 다른 의미!
- 릿지와 라쏘의 규제랑 비슷, 관련 있음. 반비례 관계
비선형 회귀 작업 -> 커널 SVM 모델
아래 그림은 이차항의 커널을 사용한 랜덤 이차원 학습 데이터에 대한 SVR 모델
입실론으로 마진의 폭을 정하고
C를 통해 모델의 설명력을 조정

- 기존 선형 회귀 분석에서는 잔차제곱합(MSE)를 최소화하는 방식으로 회귀계수를 추정함
- SVR에서는 MSE말고 다른 개념 도입
- MSE 대신 잔차 절댓값의 평균을 최소화시켜 최적의 직선을 찾는 방법도 생각할 수 있음
- 이러한 loss function을 MAE
- MAE는 MSE보다 이상치의 영향을 덜 받음
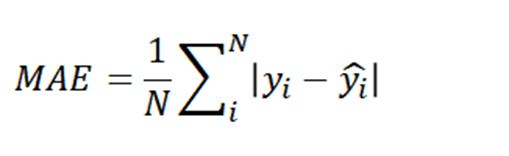


- SVR은 미리 입력한 epsilon 구간(마진) 안에 최대한 많은 데이터 포인트가 포함되도록 학습
- 도출된 loss function은 MAE에서 마진 안의 잔차들을 무시한 것과 같다
-> 그래서 마진 안에 데이터가 들어와도 모델에 영향 없는 것
- 이를 epsilon insensitive loss 라고 함

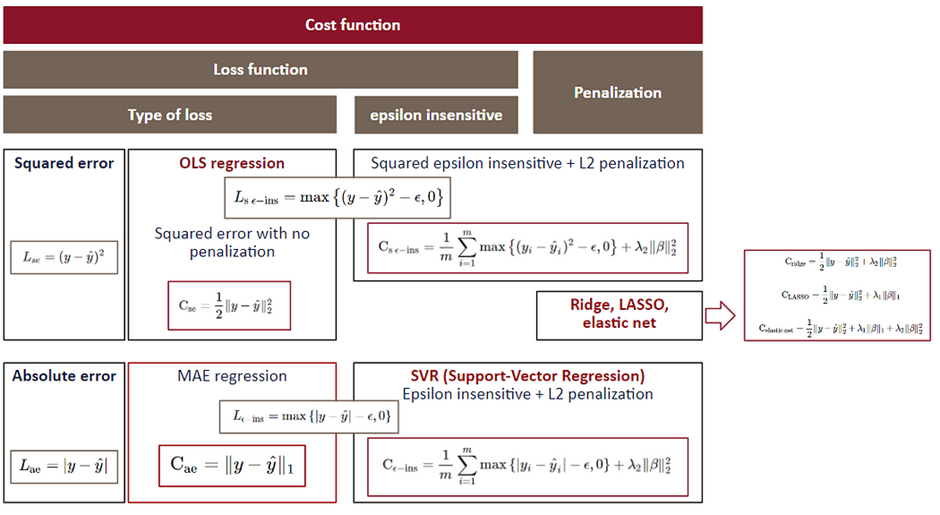

cost function의 수축항에 있는 람다는 SVR의 규제 C과 반비례 관계에 있음(뇌피셜)
C과 규제 람다에 대한 명확한 관계식은 모름
C가 크다(규제가 없다) -> 람다는 작다 -> 수축 덜 됨 -> 모델의 설명력, 복잡도 높음
C가 작다(규제가 많다) -> 람다는 크다 -> 수축 많이 됨 -> 모델의 설명력, 복잡도는 낮음
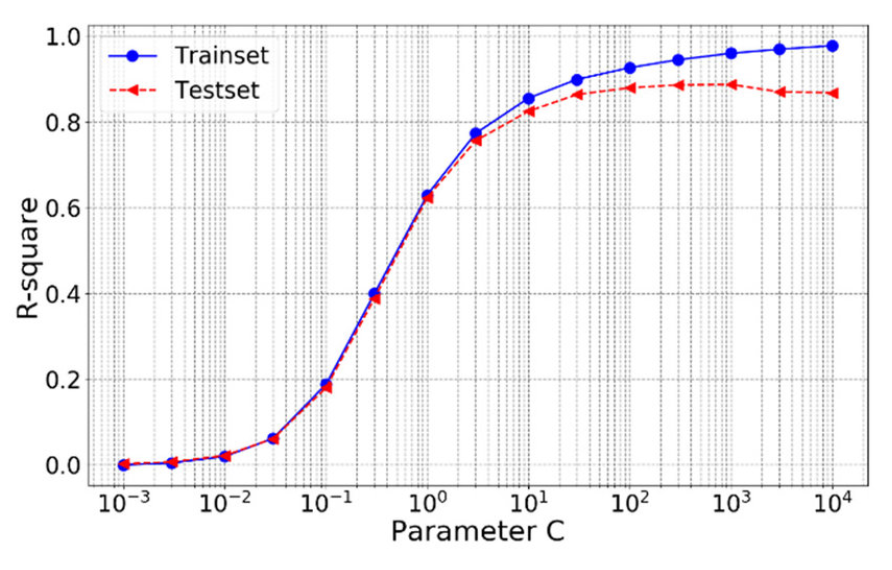
C가 커지면 규제가 없어진다는 뜻이므로
C가 커짐에 따라 모델은 점점 복잡해지고 설명력이 올라간다
따라서 R-square(설명력)도 C가 커짐에 따라 증가하는 형태를 보임
train set의 R-sqaure는 C가 커짐에 따라 계속 커짐
test set의 R-square는 C가 커짐에 따라 계속 커지진 않음. 오버피팅 문제와 관련.
결론
- 서포트 벡터 회귀는 epsilon insensitive error를 사용하는 선형 회귀로 생각할 수 있음
'Python > ML' 카테고리의 다른 글
| SVM(Support Vector Machine) (0) | 2023.03.26 |
|---|---|
| 나이브 베이즈(Naive Bayes) 분류 (0) | 2023.02.09 |

